Tweespijkerillusie

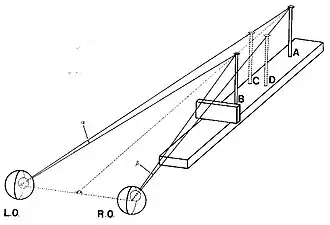
De tweespijkerillusie^[1] is een multimodale illusie waarbij twee fysieke, gelijkvormige objecten, die zich in diepte achter elkaar bevinden, visueel niet achter elkaar maar naast elkaar lijken te staan, in diepte ongeveer midden tussen de twee fysiek aanwezige objecten. Deze waarneming kan niet worden verklaard op basis van klassieke theorieën voor binoculair zien (Krol 1982, p.28-33), maar wel met binoculaire schijnbeelden in een neuraal netwerk.

De basisopstelling is in 1950 genoemd door Rønne^[2] en in 1978 herontdekt en systematisch onderzocht door Krol^[3], zie de onderzoeksgeschiedenis.^[4]

De voorwaarden voor de illusie en de belangrijkste waarnemingen zijn beschreven onder basis tweespijkerillusie, onder metingen aan schijnbeelden en onder varianten. Gerelateerde waarnemingen staan onder randen en vlakken.

Identieke beelden. Bij de basis illusie bevinden de twee objecten zich rechtop in het gezichtsveld, op dezelfde hoogte en met dezelfde lengte en kleur; en staan achter elkaar, op een lijn met de neus (Krol 1982, p.25).

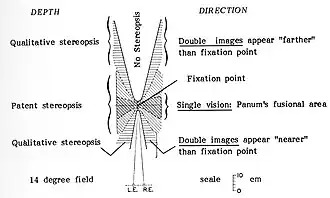
Gebied voor fijne stereopsis. Om de illusie te ervaren moeten beide echte objecten zich bevinden binnen het gebied voor fijne stereopsis (in de figuur: patente stereopsis) (Krol 1982, p.10-13). Bij een kijkafstand van 30 cm heeft dit gebied recht vooruit een bereik van slechts 7 - 22 mm^[5][6], symmetrisch rond het fixatiepunt; meer naar opzij neemt het bereik snel toe. Dit betekent dat de maximale afstand tussen beide objecten tussen 7 en 22 mm mag zijn, mits de ogen op een punt midden tussen beide objecten zijn gericht. Als de ogen op het voorste (of achterste) object zijn gericht wordt dit object als enkelbeeld, gefuseerd beeld, gezien en het andere object als dubbelbeeld zonder diepte op de kijkafstand (horopter).^[7]. Deze waarnemingen worden voorspeld door klassieke bevindingen voor binoculaire diepteperceptie. De binoculaire schijnbeelden (C,D) worden dan dus niet gezien.

Afstand. Als de kijkafstand tot de twee objecten wordt vergroot, dan neemt de diepterange in mm toe. De afstand tussen de beide objecten kan dan groter zijn. Omgekeerd, als de kijkafstand wordt verkleind dan moet de afstand tussen de objecten kleiner zijn. Door de kijkafstand te variëren kan geschakeld worden tussen het zien van de illusie en het zien van de dubbelbeelden (Krol 1982, p.27).

Convergentie. Als een waarnemer, met normaal gezichtsvermogen, zijn aandacht richt op de beide objecten, dan covergeren en accommoderen beide ogen automatisch op een punt tussen de beide objecten. Dit is meer het geval naarmate de afstand tussen beide objecten kleiner is. Op het moment dat dit gebeurt ontstaat een stabiele toestand waarbij het moeilijker is om op een andere afstand te convergeren. Dit betekent dat als de illusie eenmaal wordt gezien, het gemakkelijk is om deze te blijven zien (Krol 1982, p.29-30).

Neussteun. De illusie is zeer gevoelig voor verstoringen en is het snelste op te roepen met een kijkopstelling die precies is uitgelijnd en waarbij de positie van het hoofd is gestabiliseerd, bijvoorbeeld met een neussteun (Krol 1982, p.51). Maar het kan ook met de volgende eenvoudige demonstratie.

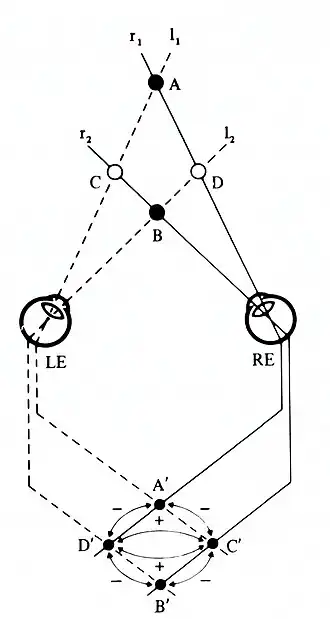
Het onderste deel van de figuur bevat een vereenvoudigde weergave van het neuromodel waarmee het onderzoek naar de tweespijkerillusie is gestart (Krol 1982, p.20). Dit model is gebaseerd op het bestaan van zenuwcellen die in de visuele cortex zijn gevonden, en die zijn afgestemd op een bepaalde binoculaire dispariteit.^[8]

In de situatie van de tweespijkerillusie worden 4 binoculaire cellen A', B', C' en D' geprikkeld die de plaats en diepte van A, B, C en D signaleren. Als er geen interactie zou zijn tussen de cellen, dan voorspelt het model dat er vier objecten zouden moeten worden waargenomen.

Om de waarneming bij de tweespijkerillusie te verklaren wordt aangenomen dat de binoculaire cellen, wanneer ze worden geactiveerd, elkaar als volgt beïnvloeden:

1. cellen die zijn afgestemd op dezelfde diepte (dispariteit) versterken elkaars activiteit (+);
2. cellen die zijn afgestemd op verschillende dieptes (dispariteiten) verzwakken elkaars activiteit (−).

Het resultaat is dat C' en D' extra geactiveerd raken en er schijnbeelden te zien zijn, en A' en B' elkaars activiteit onderdrukken en stil worden, met als gevolg dat de fysiek aanwezige objecten A en B niet worden waargenomen. Dit mechanisme zou ook de waargenomen diepte in de random dot stereogrammen van Bela Julesz^[9] kunnen verklaren.

De bovenstaande verklaring geldt voor de situatie dat de voorste en achterste stimulus zich beiden in het gebied voor binoculair dieptezien (stereopsis) bevinden. Als A en B verder uit elkaar elkaar staan en buiten dit gebied vallen, dan worden A en B volgens het model niet gezien omdat er geen binoculaire cellen zijn die geprikkeld worden. Met andere woorden, er kan en hoeft dan geen interactie tussen binoculaire cellen te zijn om de waarneming te verklaren, zoals bij onderstaand Wheatstone-stereogram.

Het bovenbeschreven model is onderdeel van een model dat naast fijne stereopsis ook enkelzien en dubbelzien omvat (Krol 1982, p. 53-79).

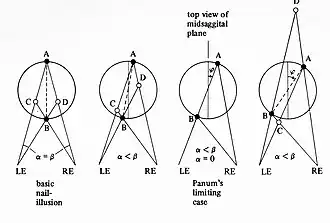
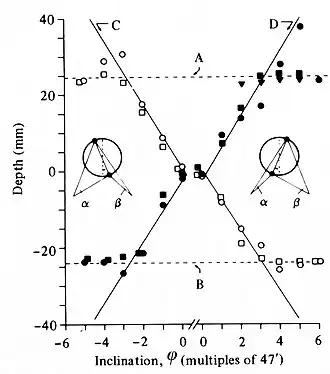
Krol (1982, p.40-48) heeft onderzoek gedaan naar de exacte positie waarop schijnbeelden worden waargenomen als de twee spijkeropstelling uit het midsagittale vlak wordt gedraaid (inclinatie), zie de figuur. Als de twee echte objecten A en B rond een punt midden tussen AB worden geroteerd, dan verschuiven de geometrische schijnbeelden C en D langzaam uit elkaar in diepte, zie linker twee plaatjes. In het derde plaatje, Panum's limiting case vallen AB en CD samen. Bij nog grotere rotatie (rechter plaatje) bewegen C en D heel snel uit uit elkaar.

Waarnemers in de experimenten dienden een vast punt te fixeren en met een aanwijsmiddel aan te geven waar zich het waargenomen linker en rechter beeld bevond. (Of de waarnemer goed fixeerde werd vastgesteld met een monoculaire nonius lijn in elk oog.)

Figuur dieptemeting toont een typische meting. In de figuur zijn de werkelijke diepteposities van A, B, C en D ten opzichte van de fixatieafstand aangegeven. De symbooltjes tonen de waargenomen diepte. Bij kleine inclinaties (rotaties) worden de waargenomen beelden op de posities van de schijnbeelden C,D gezien. Vanaf Panum's limiting case worden de beelden op de posities van de werkelijke beelden A,B gezien. Dit laatste is te verklaren doordat C,D zich dan buiten het gebied voor stereopsis bevinden.

Conclusie: bij kleine inclinaties worden (inderdaad) de binoculaire schijnbeelden (C,D) gezien. Bij inclinaties groter dan Panum's limiting case worden de echte objecten (A,B) gezien.

De hypothese dat bij de basis tweespijkerillusie binoculaire schijnbeelden worden gezien leidt tot de voorspelling van verschillende verschijningsvormen als het fixatiepunt en de afstand, kleur, vorm of de oriëntatie van de twee "spijkers" wordt gevarieerd. Deze varianten zijn inderdaad aangetoond (krol 1982, p.27-39):

• Dikteverschil: Als het voorste en achterste object ongelijk dik zijn (bijvoorbeeld 0,75 en 1,5 mm) dan worden twee gedraaide vlakken gezien waarbij de mate van draaiing wordt voorspeld door het dikteverschil (Krol 1982, p.27-28), zie figuur dikteverschil..
• Lengteverschil: Als het voorste en achterste object ongelijk lang zijn, dan treedt de illusie alleen op voor het deel dat beide objecten even hoog zijn. Het daarboven uitstekende wordt op de werkelijke positie gezien, en lijkt te zweven. Als het kortste object een bolletje heeft, dan wordt dit bolletje op de werkelijke positie gezien, en lijkt te zweven (Krol 1982, p.27-33), zie figuur lengteverschil.
• Vergentie: De illusie treedt op als de ogen tussen het voorste en achterste object convergeren, en de afstand tussen de objecten klein genoeg is.. Als de vergentie wordt verlegd van een punt midden tussen beide objecten naar het voorste of achterste object, dan wordt het gefixeerde object enkel gezien en het andere object dubbel. De illusie treedt dan niet op (Krol 1982, p.27-33).
• Inclinatie met dubbelbeeld: Als het voorste object een bolletje heeft en de afstand tussen de objecten wordt vergroot en de opstelling enige graden wordt gedraaid (inclinatie), dan kan het volgende worden gezien: het voorste bolletje verschijnt als een dubbelbeeld op de fixatieafstand, de schijnbeelden verschijnen iets daarachter en verschoven in diepte. Krol (1982, p. 32), zie figuur inclinatie met dubbelbeeld.
• Kantelen: Als het voorste en achterste object ten opzichte van elkaar in links-rechts richting kantelen, dan kantelen de waargenomen objecten in diepterichting (Krol 1982, p.36-38), zie figuur kantelen..
• Contrastverschil: als het voorste en achterste object beide lichter of donkerder zijn dan de achtergrond, dan is de diepteillusie onveranderd en onafhankelijk van het het contrast tussen beide. Als het ene object lichter is en het andere donkerder dan de achtergrond, dan is geen fusie mogelijk en worden van hetzij het voorste dan wel van het achterste object dubbelbeelden gezien, nabij de afstand van de horopter (Krol 1982, p. 39).
• Kleurverschil: als het voorste en achterste object op gelijke hoogte respectievelijk een rood en een groen bolletje hebben dan is de diepteillusie onveranderd. De bolletjes worden naast elkaar gezien waarbij op verschillende momenten de linker groen is en de rechter rood en v.v., of beide dezelfde kleur hebben. Er wordt geen kleurmenging gezien.(Krol 1982, p. 38-39).

• 
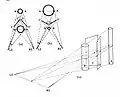  Dikteverschil geeft zwaaideuren.
• 
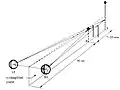  Lengteverschil. Verticale stippellijnen worden niet gezien.
• 
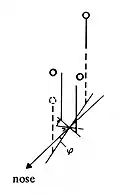  Inclinatie met dubbelbeelden.
• 
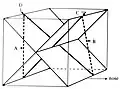  Kantelen. De vlakken dienen als hulp om het overhellen te illustreren. Kijkrichting van R naar L.

Volgens Hering (1864)^[10] detecteert het visuele systeem "randen" en vult oppervlakken in tussen deze randen. Hierbij treedt geen binoculaire kleurmenging op (Krol 1982, p. 38-39). Julesz (1971)^[9] bevestigde met stereogrammen met willekeurige stippen dat dispariteitsdetectie voorafgaat aan vormdetectie.

Elk object van de tweespijkerillusie bestaat uit een vlakje met een linker en een rechter rand, waarbij de linker rand een licht-donker overgang is en de rechter rand een donker-licht overgang, of v.v.. Krol (1982, p.81-124) heeft aangetoond dat alleen randen met dezelfde overgang in het linker en rechter oog samen een diepte ervaring geven. Bij een tegengesteld contrast is er geen dieptedetectie op basis van dispariteit en convergeren de ogen automatisch zo dat randen met tegengesteld contrast niet op corresponderende punten in beide ogen vallen. De resulterende fixatiedispariteit geeft een gering, kwalitatief diepte effect (Krol 1982, p.94-112).

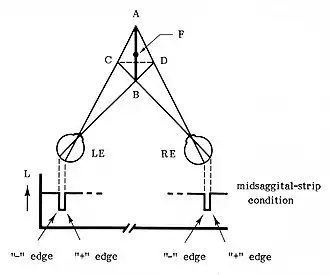
Als gevolg van de gelijk-contrast regel treedt de midsagittale-strip illusie op: als een smal vlak zoals een scheermesje in het midsagittale vlak wordt gehouden, dan hebben de randen A en B een tegengesteld contrast en de randen C en D gelijk contrast. Het schijnbare vlak CD wordt gezien en het werkelijke vlak AB niet; dit is geen tweespijkerillusie (Krol, 1982 p.84). De de gelijk-contrast regel verklaart ook de waargenomen gedraaide vlakken worden gezien als de twee objecten van de tweespijkerillusie verschillen in dikte.

Bij de demonstratie in figuur "Ambigue vlakken" kan de waarnemer geen onderscheid maken tussen het zien van een schijf op een pin boven een witte achtergrond, en een witte afgeknotte conus met een zwart top-vlak. In beide gevallen wordt afwisselend een zwarte zwevende schijf en een witte conus gezien Krol (1982, p.114) .

De tweespijkerillusie is een illusie waarbij de waarnemingen via de ogen en de tast conflicteren met elkaar en met de fysieke werkelijkheid (Krol 1982, p. 4-5). Door vanuit een andere positie te kijken kan de waarnemer op basis van visuele informatie vanuit verschillende perspectieven weten wat de “ware” situatie is. Door met een vinger te voelen, kan de waarnemer weten dat de fysieke objecten (wel) aanwezig zijn en de waargenomen objecten (schijnbeelden) niet. Als de waarnemer de oriëntatie van de twee spijkers ten opzichte van elkaar een heel klein beetje verandert, dan wordt een beweging in diepte waargenomen die niet correspondeert met de uitgevoerde beweging, zie "inclinatie" en "kantelen" bij de varianten. De fysieke objecten bij de tweespijkerillusie bevatten daarnaast, door hun fysieke afstandsverschil, subtiele monoculaire dieptecues die de ware aard van de waargenomen beelden verraden. De illusie treedt ook op als de twee fysieke objecten duidelijk door kleur van elkaar zijn te onderscheiden (bijvoorbeeld de ene rood en de andere groen); in de waarneming wisselt de kleur van de waargenomen beelden dan tussen beide kleuren. Ondanks dit alles worden (toch) de schijnbeelden gezien. Krol (1982) beschrijft dat het proberen te voelen van de schijnbeelden, en het zien van een andere beweging dan wordt uitgevoerd, een ongemakkelijk gevoel geven van “hier klopt iets niet” en een reflexmatige glimlach opwekt.

Krol (1982, p.26) beschrijft een eenvoudige manier om de illusie op te roepen met een naald en een spiegel voor het tweede object . Hierbij wordt de naald op ca 30 cm afstand gehouden, op enkele millimeters van de spiegel, waarbij een zo groot mogelijk deel van de naald zichtbaar is en de top van de naald en de top van het spiegelbeeld op gelijke hoogte worden gezien, in het verlengede van de neus.

Of de juiste situatie aanwezig is kan worden gecontroleerd door afwisselend het linker- en het rechter oog te sluiten, zonder het hoofd of de naald te bewegen, en te kijken of elk oog twee naalden ziet die vlak naast elkaar staan op zo weinig mogelijk afstand.

N.B. De opgeroepen waarneming bij het gebruik van een spiegelbeeld lijkt op, maar is niet helemaal hetzelfde als de fysieke illusie, zie multimodale illusie.

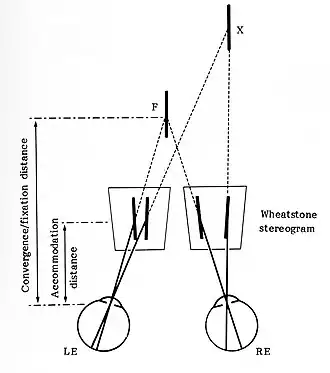
Sommige onderzoekers gebruiken een Wheatsone stereogram om de tweespijkerillusie op te roepen (Krol 1982, p.24), zie de figuur. Dit stereogram bestaat uit twee beelden, een voor elk oog, met twee parallelle lijnen. In de klassieke figuur van het Wheatstone sterogram worden alleen de posities van de schijnbeelden geillustreerd (X en F komen overeen met C en D van de tweespijkerillusie). De equivalente projecties van A en B zijn door Wheatstone niet aangeven, deze liggen ver buiten het gebied voor dieptezien. Deze situatie is daarom niet gelijk te stellen aan de situatie van de tweespijkerillusie.

Krol (1982, p.24) geeft aan dat een stereogram verschilt van de fysieke tweespijkerillusie omdat bij een stereogram geen fysieke objecten aanwezig zijn en er geen sprake is van een multimodale illusie.

Samenvattend, er kunnen twee typen objecten worden onderscheiden:

1. er is een fysiek object dat kan worden aangeraakt maar niet wordt waargenomen;
2. er wordt een object waargenomen op een positie waarop het niet kan worden aangeraakt.

Bij stereogrammen zijn er alleen fysieke objecten in de vorm van het stereogram zelf. Er zijn geen cues in het waargenomen beeld die aangeven welke objecten wel of niet echt zijn. Alle waargenomen beelden zijn van type-2. Bij de tweespijkerillusie zijn er zowel type-1- als type-2-beelden. De waarnemer kan via de tastwaarneming weten welke beelden echt zijn, maar deze informatie wordt niet gebruikt in de visuele waarneming.

Het onderzoek naar de tweespijkerillusie is op verschillende plaatsen beschreven.^{[2][11][12][13][14]} en dit onderzoek is samengevat in Krol (1982)^[3].

De waarneming van de basis tweespijkerillusie kan worden beschreven met Hering's cyclopische projectie waarbij de beelden op de kijkafstand (horopter) worden gezien; de waarneming van de varianten kan niet zo worden verklaard (Krol 1982 p.59, 89-90).

Burt en Julesz (1980)^[15] verklaren de illusie door aan te nemen dat elk object in het fusiegebied een "verboden zone" creëert waardoor andere objecten niet gefuseerd en niet gezien zouden kunnen worden. Krol en van de Grind (1982a)^[16] bestrijden dit idee. Burt en Julesz(1982)^[17] hebben hierop een antwoord, dat vervolgens weer wordt weerlegd door Krol en van de Grind(1983)^[18], zie ook Krol (1982, p.159-167).

Metingen aan de dieptepositie van de waargenomen beelden bij de verschillende varianten, bevestigen dat de waargenomen beelden binoculaire schijnbeelden zijn.^[12] Ono heeft in 1984 een alternatieve verklaring gepubliceerd^[19]. Deze alternatieve verklaring is door Krol en v.d. Grind weerlegd.^[20]

Krol en van de grind (1986)^[21] laten zien dat sommige schijnbare diepteeffecten het gevolg zijn van het feit dat de ogen proberen te voorkomen dat randen met met een tegengesteld contrast op corresponderende delen van beide ogen vallen (diepte door vergentie). Foley's alternatieve verklaring van de tweespijkerillusie op basis van "diepte-menging" zou daarmee ook ontkracht zijn. (Krol 1982, p.81-111, 125-144) argumenteren verder dat het zien van diepte in een 2-lijn stereogram met tegengesteld contrast, kan worden verklaard.

Nakazimo en Kondo(1988) hebben de overeenkomsten met het "wallpaper phenomenon" onderzocht.^[22]. Nakazimo, Shimono en Kondo (1889)^[23] hebben de tweespijkerillusie in Panum's limiting case onderzocht en komen tot vergelijkbare resultaten als gerapporteerd door Krol(1982).

• Binoculair zien
• Richtingzien
• Stereopsis (zien)
• Horopter