Horopter
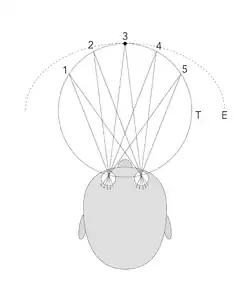
In de wetenschap van het zien heeft het begrip horopter verschillende betekenissen. In de theorie over richtingzien wordt het begrip horopter gebruikt om aan te geven welke punten in de ruimte op gelijke punten van beide netvliezen projecteren (geometrische horopter) en wordt beschreven hoe visuele richtingen worden omgezet in egocentrische richtingen. In waarnemingsonderzoek (empirisch onderzoek) wordt het begrip horopter gebruikt om aan te geven welke punten in de ruimte voldoen aan een bepaald waarnemingscriterium, zoals: fusie (enkelzien), gelijke richting in beide ogen, gelijke diepte als het fixatiepunt en afwezigheid van een oogbewegingsreflex (vergentiereflex). Welke definitie wordt bedoeld wordt aangeven door een verwijzing naar het toegepaste criterium, zoals fusiehoropter, richtinghoropter, dieptehoropter (of dispariteithoropter) en vergentiehoropter. Afhankelijk van de definitie kan de horopter een lijn zijn, een gebogen vlak of een aaneengesloten gebied in de ruimte.
Geometrische horopter
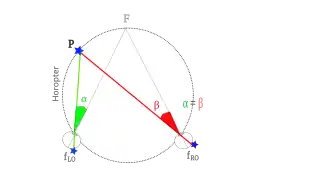
In een plat vlak door beide ogen is de horopter een cirkel door beide ogen en het fixatiepunt (Vieth-Müllercirkel). Ruimtelijk is de horopter een vlak dat zich ook verticaal uitstrekt.
De geometrische horopter is uitgevonden als een hulpmiddel (model) om empirisch onderzoek te doen aan het zien van richting en diepte.
De geometrische horopter brengt in beeld welke netvliespunten in beide ogen anatomisch corresponderende punten zijn en kijken in gelijke visuele richtingen, zie de tekening.
De horopter brengt ook in beeld welke punten in de ruimte zich geometrisch op gelijke diepte als het fixatiepunt bevinden. Deze punten hebben een binoculaire dispariteit van nul en dus gelijke visuele richtingen. Het zijn dus (ook) punten op de horopter.
Horopter als scherm
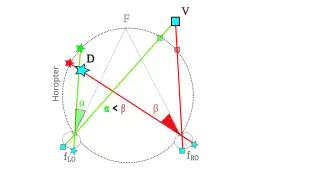
In vroege theorieën wordt de geometrische horopter voorgesteld als een scherm waarop de omgeving wordt waargenomen. Punten die dichterbij (D) of verderaf (V) liggen, raken het scherm op twee verschillende punten.
Hoewel het bovengenoemde scherm niet echt bestaat, geeft het wel een correcte beschrijving van hoe dubbelbeelden worden gezien. In het geval dat de richtingen van beide ogen kruisen voor de horopter (punt D), is het linker dubbelbeeld afkomstig van het rechter oog en v.v. Deze situatie staat bekend als "gekruiste dispariteit". Bij een punt verder weg dan de horopter wordt het beeld van het linker oog links gezien van het beeld van het rechter oog. Onderzoekers noemen dit "parallele dispariteit". En bij een punt op de horopter vallen de twee richtingen samen en en wordt er dus maar 1 beeld gezien.
Empirische horopter
In waarnemingsonderzoek is met verschillende criteria gemeten of en hoe de empirische horopter afwijkt van de geometrische horopter. Zo blijkt de vorm afhankelijk van de fixatieafstand: bij grotere fixatie-afstanden is de vorm niet concaaf (hol) zoals bij de geometrische horopter, maar plat of convex (bol). Ook buigt de verticale horopter boven het fixatiepunt naar de waarnemer toe en onder het fixatiepunt van de waarnemer af. Er wordt algemeen aangenomen dat deze variaties het gevolg zijn van de manier waarop onze ogen bewegen in de oogkassen en aanpassingen zijn aan de omgeving.[1][2]
In het volgende worden enkele voorbeelden gegeven van het meten aan verschillende empirische horopters en wat daarbij is gevonden. Het gebruik van de term "horopter" is niet in al deze gevallen intuïtief. Om deze reden wordt naast of in plaats van de term voor de empirische horopter soms ook een andere term gebruikt. Bijvoorbeeld, de te bespreken fusiehoropter wordt door veel onderzoekers (ook) Panum's fusiegebied genoemd.
Fusiehoropter
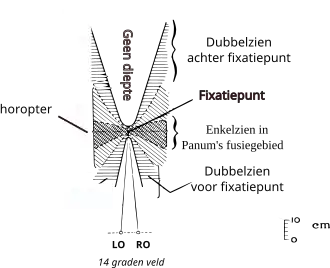
Volgens Hering's projectie hebben alle punten die niet op de horopter liggen verschillende visuele richtingen in elk oog. De overeenkomstige richtingen in het cyclopische oog zijn dus ook verschillend en dus dubbel, naast elkaar aanwezig in het cyclopisch beeld. Uit waarnemingsonderzoek blijkt dat sommige van deze beelden toch niet dubbel, maar enkel worden gezien, in een richting die tussen de twee visuele richtingen in ligt. Dit verschijnsel wordt fusie (samensmelten) genoemd.
Het optreden van fusie is door Panum, Ogle en anderen gemeten door een verticale staaf in de ruimte te verplaatsen en vast te stellen wanneer de staaf enkel of dubbel wordt waargenomen. Het resultaat is geen lijn, zoals de geometrische horopter, maar een gebied dat zich uitstrekt aan weerszijden van de geometrische horopter. Dit gebied wordt Panum's fusiegebied genoemd. Zij vonden ook dat dubbelbeelden met een grote dispariteit op de horopter worden gezien, en dubbelbeelden met kleinere dispariteiten (iets) verder weg of dichter bij dan de horopter; de dieptesensatie is minder levendig en minder groot dan bij gefuseerde beelden.[3]
Het bestaan van fusie wordt niet verklaard door de klassieke theorie. Theorieën die gebruik maken van het feit dat er in de visuele cortex neuronen zijn gevonden die via elk oog in een bepaalde visuele richting kijken, kunnen dit verschijnsel wel verklaren.[4]
Richtinghoropter
De cyclopische projectie van Hering gaat er van uit dat geometrisch gelijke visuele richtingen uitmonden in een gelijke egocentrische richting. Dit, en de verschuiving van de richting bij fusie, zijn gemeten door twee veritcale staven op ongelijke hoogte (boven elkaar) in de ruimte te bewegen tot ze recht boven elkaar worden gezien. Als de ene staaf alleen door het ene oog en de andere staaf door het andere oog wordt gezien, dan wordt deze methode nonius-methode genoemd. Hiermee is o.a. vastgesteld dat bij fusie de egocentrische richting in licht tussen de monoculaire visuele richtingen; bij een sterk dominant oog ligt deze richting dichter bij de richting die door het dominante oog wordt gezien.[5]
Dieptehoropter
In de theorie naar dieptezien wordt er van uitgegaan punten op de horopter dezelfde diepte hebben als het fixatiepunt. Dit is onderzocht door een diepte-aanwijzer in de ruimte te bewegen en vast te stellen op welk punt deze op gelijke diepte met het fixatiepunt wordt gezien. Het resultaat is een lijn die midden door Panum's fusiegebied loopt.[3]
Vergentiehoropter
Zodra een punt dat de aandacht heeft buiten Panum's fusiegebied dreigt te komen, zorgt een automatische oogbeweging (vergentiebeweging) dat het punt weer midden in Panum's fusiegebied komt te liggen. In onderzoek naar deze reflex wordt de vergentiehoropter gedefinieerd als de verzameling punten binnen Panum's fusiegebied die geen reflex opwekken. De gemeten horopter valt centraal binnen het fusiebereik van Panum. In het verticale vlak staat de vergentiehoropter minder schuin dan het corresponderende fusiebereik.[6]
Geschiedenis
De term 'horopter' werd in 1613 geïntroduceerd door Franciscus Aguilonius.[7] In de 19e eeuw werd de geometrische cirkel in het horizontale vlak bekend als de 'Vieth-Müllercirkel' , hoewel Johannes Müller al verwachtte dat de horopter een oppervlak in de ruimte zou zijn, d.w.z. niet beperkt tot het horizontale vlak. In 1838 vond Charles Wheatstone de stereoscoop uit, waarmee hij en anderen de empirische horopter konden onderzoeken.[8][9] Later hebben Hermann von Helmholtz en Ewald Hering vrijwel gelijktijdig de exacte vorm van de horopter uitgewerkt.[10][11] Daarna hebben anderen laten zien dat de theoretische/geometrische horopter met de Vieth-Müllercirkel een benadering is.[12][13][10][11][14][15][16][17]
Zie ook
Referenties
- ↑ Sprague (2015). Stereopsis is adaptive for the natural environment. Science Advances 1 (4): e1400254. PMID 26207262. PMC 4507831. DOI: 10.1126/sciadv.1400254.
- ↑ Gibaldi (2017). The Active Side of Stereopsis: Fixation Strategy and Adaptation to Natural Environments. Scientific Reports 7. PMID 28317909. PMC 5357847. DOI: 10.1038/srep44800.
- ↑ a b c Ogle K. N. (1950), "Researches in binocular vision", Philadelphia: Saunders.
- ↑ Krol J.D.(1982), "Perceptual ghosts in stereopsis, a ghosly problem in binocular vision", PhD thesis ISBN 90-9000382-7.
- ↑ Hariharan-Vilupurua S.L.;Bedella H. (2008), "The perceived visual direction of monocular objects in random-dot stereograms is influenced by perceived depth and allelotropia”, Vision Research 49 (2009) 190–201
- ↑ Harrold A.L.; Grove P.M. (2021),"The vergence horopter", Vision Research Volume 180, March 2021, Pages 63-79 [1]
- ↑ Aguilonius, Franciscus. Opticorum libri sex.
- ↑ Glanville, AD (1993). The Psychological Significance of the Horopter. The American Journal of Psychology 45 (4): 592–627. DOI: 10.2307/1416191.
- ↑ Wheatstone, C (1838). Contributions to the Physiology of Vision. Part the First. On Some Remarkable, and Hitherto Unobserved, Phenomena of Binocular Vision. Philosophical Transactions of the Royal Society of London 128: 371–94. DOI: 10.1098/rstl.1838.0019.
- ↑ a b Howarth, PA (2011). The geometric horopter. Vision Research 51 (4): 397–9. PMID 21256858. DOI: 10.1016/j.visres.2010.12.018.
- ↑ a b Tyler, Christopher W (1991). De horopter en binoculaire fusie. In Vision and visual dysfunction 9., 19–37.
- ↑ Gulick, W L, Lawson, R B (1976). Human Stereopsis: A psychophysical analysis. Oxford University Press, New York.
- ↑ Turski, Jacek (2016). On binocular vision: The geometric horopter and Cyclopean eye. Vision Research 119: 73–81. PMID 26548811. DOI: 10.1016/j.visres.2015.11.001.
- ↑ Howard, Ian P, Rogers, Brian J (2002). Seeing in depth, volume 2: Depth perception. I. Porteous, Ontario, Canada.
- ↑ Solomons, H (1975). Derivation of the space horopter. The British Journal of Physiological Optics 30 (2–4): 56–80. PMID 1236460.
- ↑ Solomons, H (1975). Properties of the space horopter. The British Journal of Physiological Optics 30 (2–4): 81–100. PMID 1236461.
- ↑ Schreiber, KM, Tweed, DB, Schor, CM (2006). The extended horopter: Quantifying retinal correspondence across changes of 3D eye position. Journal of Vision 6 (1): 64–74. PMID 16489859. DOI: 10.1167/6.1.6.