Stelling van Marden

■ de drie nulpunten $1+i,\ 5+2i$ en $3+6i$ van $z^{3}-(9+9i)z^{2}+(3+52i)z+33-39i$

■ de twee nulpunten
$3{,}32+4{,}05i$ en $2{,}68+1{,}95i$
van de afgeleide

■ de drie raakpunten aan de ingeschreven ellips

De stelling van Marden is een stelling uit de complexe functietheorie. De stelling legt een meetkundig verband in het complexe vlak tussen de nulpunten van een derdegraadspolynoom en de nulpunten van de afgeleide ervan. De coëfficiënten van het polynoom mogen complexe getallen zijn. De stelling is naar Morris Marden genoemd. Marden schreef de stelling toe aan Jörg Siebeck.^[1]

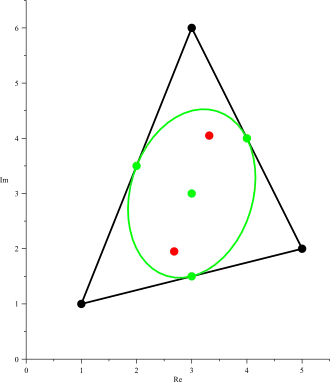
De nulpunten van de afgeleide van een derdegraadspolynoom, waarvan de nulpunten niet op één lijn liggen, zijn de brandpunten van Steiners ingeschreven ellips van de driehoek die door die nulpunten wordt gevormd. De raakpunten van de ingeschreven ellips van Steiner in de driehoek liggen op de middens van de zijden van die driehoek. Volgens de stelling van Gauss-Lucas liggen alle nulpunten van de afgeleide van een polynoom in een convexe veelhoek, als ook alle nulpunten van het polynoom zelf in die convexe veelhoek liggen.

voetnoten

↑ Jörg Siebeck. Über eine neue analytische Behandlungweise der Brennpunkte, 1864. in Journal für die reine und angewandte Mathematik vol 64 blz 175–182

literatuur

Morris Marden A note on the zeroes of the sections of a partial fraction, 1945. in Bulletin of the American Mathematical Society vol 51, 12, blz 935–940 DOI:10.1090/S0002-9904-1945-08470-5

[1] Jörg Siebeck. Über eine neue analytische Behandlungweise der Brennpunkte, 1864. in Journal für die reine und angewandte Mathematik vol 64 blz 175–182

[1]