Symmetriegroep van de kubus
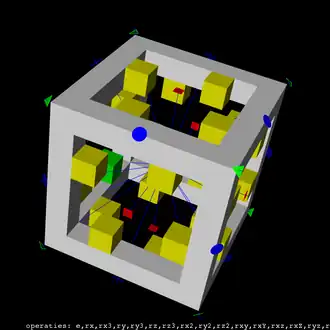
Volledig rotatiesymmetrische kubus met 24 isometriën, rotaties van
De kubus heeft octahedrale symmetrie. De kubus is 48-voudig symmetrisch: er zijn 48 verschillende bewerkingen in de symmetriegroep van de kubus die de kubus onveranderd blijft.
Een kubus is meervoudig symmetrisch omdat er verschillende soorten isometrie zijn, de rotaties om de assen van orde twee, drie en vier en verschillende spiegelingen, waarna de kubus er hetzelfde uitziet: de originele kubus en de beeldkubus zijn hetzelfde. Die transformaties zijn de symmetrieën van een kubus. De verzameling van al deze transformaties is de symmetriegroep van de kubus: . bestaat uit 48 verschillende symmetrische transformaties.
Een kubus die op een bepaalde manier is beschilderd kan behalve 48-voudig symmetrisch ook asymmetrisch zijn of een beperkte symmetrie hebben. Die symmetrie is dan een van de ondergroepen van de symmetriegroep van de kubus. De volledige octahedrale symmetrie wordt met aangegeven en en de chirale symmetrie met .
Ondergroepen
is een wiskundige groep, de symmetriegroep van de kubus.
Als we een kubus beschilderen of op een andere manier markeringen aanbrengen, dan is die kubus daarna mogelijk minder symmetrisch. Dat kan variëren van asymmetrisch tot nog steeds volledig symmetrisch overeenkomstig de blanco kubus. Maar de verzameling symmetrieoperaties is ook na beschildering een wiskundige groep. Deze symmetriegroep van een beschilderde kubus is een ondergroep van . heeft 97 ondergroepen.
Bewerkingen
De eenvoudigste isometrie is de identiteit, de bewerking die niets doet. De rotatiesymmetrieën van de kubus zijn de rotaties om de assen door de middens van twee tegenover elkaar liggende ribben, om de lichaamsdiagonalen en om de diagonalen door de middens van twee tegenover elkaar liggende zijvlakken. Het zijn er bij elkaar 23, omdat de identiteit hierbij niet telt. Zes van deze rotaties hebben orde vier, acht hebben er orde drie en negen orde twee. De kubus is niet spiegelsymmetrisch ten opzichte van een vlak loodrecht op een lichaamsdiagonaal. De puntspiegeling ten opzichte van het middelpunt van de kubus heeft geen spiegelvlak, maar kan worden gezien als drie opeenvolgende spiegelingen in de drie loodrecht op elkaar staande middenvlakken van de kubus. De chiraliteit van de puntspiegeling is daarom omgekeerd aan die van de rotaties, dus is het zelf geen rotatie. Er zijn negen spiegelingen met een spiegelvlak. Er zijn in behalve rotaties en spiegelingen ook draaispiegelingen. Een draaispiegeling is een vlakspiegeling gevolgd door een rotatie om de normaal op het spiegelvlak.[1] Er zijn zes draaispiegelingen van de orde vier en acht van de orde zes.
Alle isometriën van de kubus met hun orde staan in een tabel van de isometriën in de symmetriegroep van de kubus bij elkaar.
Symmetriesoorten van een kubus
De 97 ondergroepen van zijn verdeeld over 32 klassen van geconjugeerde ondergroepen, inclusief de triviale ondergroep met alleen de identiteit. De ondergroepen in een klasse zijn verwisselbaar middels conjugatie. Ondergroepen die tot verschillende klassen behoren kunnen niet worden verwisseld. Deze klassen van geconjugeerde ondergroepen zijn disjunct. Samen met zelf vormen deze 32 klassen de 33 symmetriesoorten van de kubus.
Dit betekent dat als we een kubus beschilderen die kubus een van deze 33 symmetriesoorten heeft. Een symmetriesoort met verschillende ondergroepen in de conjugatieklasse heeft daarmee verschillende beschilderingen van de kubus die in essentie dezelfde symmetrie zijn.
Elke ondergroep in een symmetriesoort heeft hetzelfde aantal symmetrische operaties. De orde van de symmetriesoort is het aantal operaties in elke ondergroep.
Afbeelding en tabel van de symmetriesoorten
Afbeelding

Ontbrekend: Volledig (48-voudig) symmetrisch.
Tabel
| code | orde | #OGn | OG(vb) | Beschrijving | |
|---|---|---|---|---|---|
| 1 | r1Asym | 1 | 1 | <e> | asymmetrisch |
| 2 | r22As | 2 | 3 | <rx2> | rotatie om een (coördinaat)as over 180° |
| 3 | r44As | 4 | 3 | <rx> | rotatie om een (coördinaat)as over 90° |
| 4 | r22Diag | 2 | 6 | <rxy> | rotatie om een diagonaal |
| 5 | r33Lich | 3 | 4 | <rxyz> | rotatie om een lichaamsdiagonaal |
| 6 | r222As | 4 | 1 | <rx2,ry2> | rotatie om alle coördinaatassen over 180° |
| 7 | r222DiagAs | 4 | 3 | <rxy,rxY> | rotatie om twee (overeenkomstige) diagonalen |
| 8 | r332LichAs | 12 | 1 | <rxyz,rxYZ> | rotatie om alle lichaamsdiagonalen |
| 9 | r422AsDiag | 8 | 3 | <rx,ry2> | rotaties om alle coördinaatassen |
| 10 | r322LichDiag | 6 | 4 | <rxy,rxz> | rotatie om twee diagonalen |
| 11 | r432Alle | 24 | 1 | <rx,ry> | volledig rotatiesymmetrisch |
| 12 | s11As | 2 | 3 | <sx> | spiegeling t.o.v. een (coördinaat)as |
| 13 | s11Diag | 2 | 6 | <sxy> | spiegeling t.o.v. een diagonaal |
| 14 | s22As | 4 | 3 | <sx,sy> | spiegeling t.o.v. 2 coördinaatassen |
| 15 | s44As | 8 | 3 | <sx,sxy> | alle spiegelingen 1 coördinaatas |
| 16 | s22Diag | 4 | 3 | <sxy,sxY> | spiegeling t.o.v. 2 (overeenkomstige) diagonalen |
| 17 | s33Lich | 6 | 4 | <sxY,sxZ> | alle spiegelingen rond een lichaamsdiagonaal |
| 18 | s22DiagAs | 4 | 6 | <sz,sxY> | spiegeling t.o.v. as + diagonaal |
| 19 | s332LichDiag | 24 | 1 | <sxy,rxyz> | spiegeling t.o.v. alle (lichaams)diagonalen |
| 20 | s222As | 8 | 1 | <sx,rx2,ry2> | spiegeling t.o.v. alle assen |
| 21 | s422As | 16 | 3 | <sx,rx,ry2> | spiegelingen t.o.v. alle assen |
| 22 | s222DiagAs | 8 | 3 | <sxy,rxy,rxY> | spiegeling t.o.v. 2 diagonalen en een as |
| 23 | r2s11As | 4 | 3 | <sx,rx2> | spiegeling+rotatie t.o.v. een as |
| 24 | r4s11As | 8 | 3 | <sx,rx> | spiegeling+rotatie t.o.v. een as |
| 25 | r2s11Diag | 4 | 6 | <sxy,rxy> | spiegeling+rotatie t.o.v. diagonaal |
| 26 | r2s2AsDiag | 8 | 3 | <sxy,rx2> | diagonaalspiegelingen en asrotaties |
| 27 | r2s2DiagAs | 8 | 3 | <sx,rxy> | asspiegelingen en diagonaalrotaties |
| 28 | r3s2LichAs | 24 | 1 | <sx,rxyz> | alle asspiegelingen + alle lichaamsdiagonaalrotaties |
| 29 | r2s3DiagLich | 12 | 4 | <rxy,sxz> | alle spiegelingen rond een lichaamsdiagonaal |
| 30 | sx | 2 | 1 | <sO> | puntspiegeling |
| 31 | r2sxAs | 4 | 3 | <rsx> | draaispiegeling t.o.v. een as |
| 32 | r3sxLich | 6 | 4 | <rsxyz> | draaispiegeling t.o.v. een lichaamsdiagonaal |
| 33 | s432Alle | 48 | 0 | <sx,rxy> | volledige symgroep |
Legenda:
- OG = ondergroep
- #OGn = aantal ondergroepen
- OGvb: de genoemde operaties genereren een van de ondergroepen van de symmetriesoort
Als een beschilderde kubus rotatiesymmetrisch is rond een lichaamsdiagonaal, dan is dat voor elk van de vier lichaamsdiagonalen een andere ondergroep, bij dezelfde symmetriesoort: r33Lich.
Symmetriesoort code
In bovenstaande tabel wordt bij elke symmetriesoort een code gegeven die iets zegt over de aard ervan. De code is gebaseerd op de door J.H. Conway bedachte orbifoldhandtekening.[2] Die code is hier een beetje aangepast en bovendien aangevuld. In plaats van kleuren hebben de codes hier een r voor rotatiesymmetrisch en een s voor spiegelsymmetrisch. De code is aangevuld met As, Diag en/of Lich. Per symmetriesoort bij Conway kunnen bij de kubus meer symmetriesoorten voorkomen, omdat een kubus weliswaar topologisch equivalent is met een bol, maar een rotatie om een coördinaatas iets anders is dan een rotatie om een diagonaal, anders dan een rotatie om een lichaamsdiagonaal. Hetzelfde geldt voor spiegelingen, afhankelijk van de normaal op het spiegelvlak: coördinaatas, diagonaal of lichaamsdiagonaal. De code begint met een aanduiding van de aard van de symmetriesoort gebaseerd op de Conwaycode. Daarachter komt een aanduiding van de richting van de rotaties en spiegelingen waaruit de symmetriesoort is opgebouwd. Die aanvulling is niet altijd eenvoudig uit het totaal van de symmetrieën op te maken.
Symmetriesoorten volgens Conway
Conway onderscheidt op een boloppervlak 14 symmetriesoorten.[3]
| 5 rotatiesymmetriesoorten | |||||
|---|---|---|---|---|---|
| Conway notatie | 532 | 432 | 332 | 22N | NN |
| Aangepaste notatie | r532 | r432 | r332 | rN22 | rNN |
| 5 spiegelsymmetriesoorten | |||||
| Conway notatie | *532 | *432 | *332 | *22N | *NN |
| Aangepaste notatie | s532 | s432 | s332 | sN22 | sNN |
| 4 hybride symmetriesoorten | |||||
| Conway notatie | 3*2 | 2*N | N* | Nx | |
| Aangepaste notatie | r3s2 | r2sN | rNs11 | rNsx | |
33 symmetriesoorten van de kubus per Conwaycode
De symmetriesoorten r532 en s532 komen bij de kubus niet voor.
| r432 | r332 | rN22 | rNN |
|---|---|---|---|
| r432Alle | r332LichAs | r222As | r1Asym |
| r222DiagAs | r22As | ||
| r22Diag | |||
| r322LichDiag | r33Lich | ||
| r422AsDiag | r44As | ||
| s432 | s332 | sN22 | sNN |
| s432Alle | s332LichDiag | s11As | |
| s11Diag | |||
| s222As | s22As | ||
| s22Diag | |||
| s222DiagAs | s22DiagAs | ||
| s33Lich | |||
| s422As | s44As | ||
| r3s2 | r2sN | rNs11 | rNsx |
| r3s2LichAs | sx | ||
| r2s2DiagAs | r2s11As | r2sxAs | |
| r2s2AsDiag | r2s11Diag | ||
| r2s3DiagLich | r3sxLich | ||
| r4s11As |
Polykubussen
Deze 33 symmetriesoorten zijn niet alleen van belang voor een kubus die is beschilderd . Ze gelden ook voor figuren die zijn opgebouwd uit kubussen, zoals polykubussen. De meeste polykubussen zijn asymmetrisch, maar vele hebben een of andere symmetrie. Die symmetrie is altijd een van deze 33 symmetriesoorten.
- literatuur
- JH Conway, H Burgiel en Goodman-Strauss. The Symmetries of Things, 2008
- J vd Craats. Symmetrie op de bol en in het vlak, NAW december 2011, blz 241-252
- J vd Craats. Een passie voor symmetrie, Epsilon Uitgaven, 2014
- voetnoten