Stelling van De Gua

De stelling van De Gua is een stelling die geldt als driedimensionale uitbreiding van de stelling van Pythagoras. De stelling is naar Jean Paul de Gua de Malves (1713–1785) genoemd, die de stelling in 1783 bij de Parijse Academie van Wetenschappen heeft uitgelegd. Onder meer René Descartes en Johannes Faulhaber kenden de stelling eerder en in 1774 was er bij dezelfde Academie al over dezelfde stelling in meer dimensies gesproken.

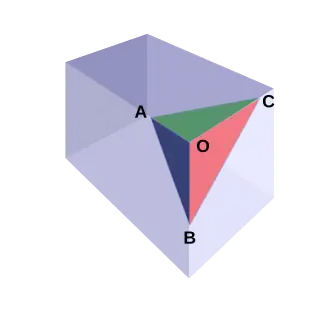
De stelling zegt dat in een viervlak ${\displaystyle OABC}$ met bij hoekpunt ${\displaystyle O}$ drie rechte hoeken, zodat het viervlak is te zien als afgesneden van een balk, geldt, dat het kwadraat van de oppervlakte van het zijvlak tegenover ${\displaystyle O}$ gelijk is aan de som van de kwadraten van de oppervlakten van drie overige zijvlakken:

${\displaystyle A_{ABC}^{2}=A_{\color {blue}ABO}^{2}+A_{\color {green}ACO}^{2}+A_{\color {red}BCO}^{2}}$

Deze stelling is evenals de stelling van Pythagoras een bijzonder geval van een stelling die geldt voor elke n-simplex met een hoekpunt, waarin alle samenkomende ribben onderling loodrecht op elkaar staan.

• (en) MathWorld. de Gua's Theorem.
• (en) Sergio A. Alvarez, Note on an n-dimensional Pythagorean theorem. , Carnegie Mellon University