Sinc-functie

De sinc-functie, of voluit met de Latijnse naam sinus cardinalis, genoteerd als sinc, is een wiskundige functie die het quotiënt is van de sinus en het argument van de sinus. De sinc-functie is de fouriergetransformeerde van een rechthoekig signaal en omgekeerd. De functie is niet alleen in de wiskunde van belang, zoals bij het bepalen van sommige limieten, maar speelt ook, vanwege de genoemde eigenschap, een belangrijke rol in de elektronica, meer bepaald in de analoge en digitale signaalverwerking alsook in de golfoptica bij diffractie. De sinc-functie is door de Brit PM Woodward in 1952 ingevoerd. Hij vond dat de functie zo vaak in fourieranalyse voorkwam, dat die een eigen naam verdiende.

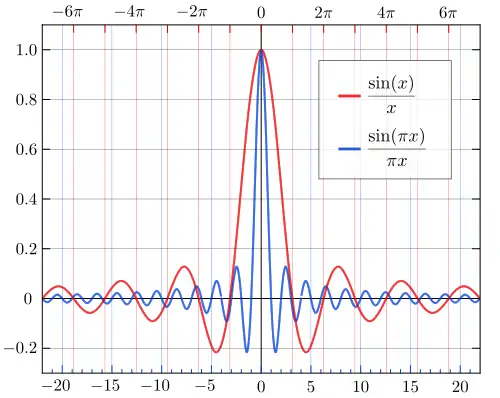
Hoewel er in de literatuur geen eenduidigheid is over de definitie van de sinc-functie, is de gebruikelijke definitie de functie die voor ${\displaystyle x\in \mathbb {R} }$ wordt gegeven door:

${\displaystyle \operatorname {sinc} (x)={\begin{cases}{\dfrac {\sin(x)}{x}},&\quad x\neq 0\\\\\quad 1,&\quad x=0\end{cases}}}$

Deze functie is symmetrisch ten opzichte van de ${\displaystyle y}$-as. Vanwege de voorgeschreven waarde in 0 is ze overal continu en differentieerbaar. De functie is nul in alle van nul verschillende veelvouden van ${\displaystyle \pi }$.

Er is ook een genormaliseerde vorm van de sinc-functie:

${\displaystyle \operatorname {sinc} (x)={\begin{cases}{\dfrac {\sin(\pi x)}{\pi x}},&\quad x\neq 0\\\\\quad 1,&\quad x=0\end{cases}}}$

De genormaliseerde vorm is nul in de gehele getallen verschillend van nul.

De genormeerde vorm van de sinc-functie laat zich met behulp van de gammafunctie uitdrukken als het product:

${\displaystyle {\frac {\sin(\pi x)}{\pi x}}=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{n^{2}}}\right)={\frac {1}{\Gamma (1+x)\Gamma (1-x)}}}$

De taylorreeks kan direct uit de taylorreeks voor de sinus worden afgeleid:

${\displaystyle {\frac {\sin(x)}{x}}=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{2n}}{(2n+1)!}}=1-{\frac {x^{2}}{6}}+{\frac {x^{4}}{120}}\mp \ldots }$

De sinc-functie is continu in het punt 0, want de limiet voor ${\displaystyle x}$ naar nul is gelijk aan 1:

${\displaystyle \lim _{x\to 0}{\frac {\sin(x)}{x}}=1}$

Dus:

${\displaystyle \lim _{x\to 0}{\frac {\tan(x)}{x}}=1}$

Soortgelijke limieten gelden ook voor de corresponderende cyclometrische functies:

${\displaystyle \lim _{x\to 0}{\frac {\arcsin(x)}{x}}=1}$

Dus:

${\displaystyle \lim _{x\to 0}{\frac {\arctan(x)}{x}}=1}$

Voor de hyperbolische functies ${\displaystyle \sinh }$ en ${\displaystyle \tanh }$ geldt:

${\displaystyle \lim _{x\to 0}{\frac {\sinh(x)}{x}}=1}$

${\displaystyle \lim _{x\to 0}{\frac {\tanh(x)}{x}}=1}$

Indien in een ${\displaystyle n}$-tal equidistente punten ${\displaystyle (x_{k})}$ met onderlinge afstand ${\displaystyle d}$ de functiewaarden ${\displaystyle (f(x_{k}))}$ gegeven zijn, kan een interpolerende functie worden geschreven als:

${\displaystyle g(x)=\sum _{k=1}^{n}f(x_{k})\ \operatorname {sinc} \left({\frac {\pi (x-x_{k})}{d}}\right)}$

Voor alle ${\displaystyle m=1,\ldots ,n}$ geldt:

${\displaystyle g(x_{m})=f(x_{m})}$,

aangezien

${\displaystyle \operatorname {sinc} \left({\frac {\pi (x_{m}-x_{k})}{d}}\right)=\operatorname {sinc} ((m-k)\pi )={\begin{cases}1,&m=k\\0,&m\neq k\end{cases}}}$

Dit soort interpolatie wordt bijvoorbeeld gebruikt bij DA-conversie van geluidsignalen.

De fouriergetransformeerde van een geschaalde sinc-functie ${\displaystyle \mathrm {sinc} (\pi t/T)}$ is gelijk aan:

${\displaystyle \int _{-\infty }^{\infty }\mathrm {sinc} (\pi t/T)\,e^{-j\omega t}\,{\rm {d}}t=T}$

op het interval

${\displaystyle [-\pi /T,\pi /T]}$

en nul daarbuiten.

Omgekeerd is de fouriertransformatie van een rechthoekig signaal in de tijd, een ${\displaystyle \mathrm {sinc} }$ in functie van de frequentie. Dit betekent dat de convolutie van een signaal met een ${\displaystyle \mathrm {sinc} }$ overeenstemt met het product van hun respectievelijke fourier-getransformeerden. Omdat de fouriertransformatie van een ${\displaystyle \mathrm {sinc} }$ echter rechthoekig is, en bijgevolg nul boven een bepaalde grensfrequentie, betekent dit dat convolutie met een ${\displaystyle \mathrm {sinc} }$ tot gevolg heeft dat frequenties hoger dan deze grensfrequentie uit het oorspronkelijk signaal verwijderd worden.

De ${\displaystyle \mathrm {sinc} }$-functie ligt dan ook aan de basis van het ontwerpen van bandselectieve filters. Dit zijn filters die bepaalde frequentiebanden doorlaten en andere banden onderdrukken. Men onderscheidt in deze context laagdoorlaatfilters, hoogdoorlaatfilters, banddoorlaatfiters en bandstopfilters.