Regelmatige zeshoek

Een regelmatige zeshoek is een regelmatige veelhoek met zes gelijke hoeken en zes gelijke zijden. Een zeshoek of hexagoon, Oudgrieks: ἕξ, hex, zes en γωνία, gonia, hoek, in het algemeen is een figuur met zes hoeken en zes zijden. De hoeken van een regelmatige zeshoek zijn 120° = 180° – 360°/6. De regelmatige zeshoek kan worden gezien als samengesteld uit zes gelijkzijdige driehoeken. Zoals het honingraatpatroon laat zien, is de regelmatige zeshoek een van de regelmatige veelhoeken die zonder verlies een vlak kunnen vullen. De andere zijn de gelijkzijdige driehoek en het vierkant.

Het is eenvoudig een regelmatige zeshoek te construeren met passer en liniaal. Zeshoeken hebben een kleine omtrek ten opzichte van hun oppervlakte, kleiner dan de andere regelmatige vlakvullende veelhoeken. Marcus Terentius Varro schreef daar in 36 v.Chr. al over en ook Pappos van Alexandrië was ermee bekend. TC Hales bewees in 1999 het honingraat-vermoeden. Hij toonde aan dat regelmatige zeshoeken de zuinigste manier geven om een vlak te vullen met figuren van hetzelfde oppervlak: een verdeling met minder omtreklengte is onmogelijk.^[1]

Regelmatige zeshoeken worden in de techniek gebruikt voor zeskantmoeren en -bouten, die met een bijpassende sleutel kunnen worden aangedraaid.

Voor een regelmatige zeshoek met zijde ${\displaystyle z}$ is:

straal van de omgeschreven cirkel	${\displaystyle R=z}$
omtrek	${\displaystyle O=6\ z}$
breedte	${\displaystyle B=2\ z}$
hoogte	${\displaystyle H={\sqrt {3}}\ z}$
oppervlakte	${\displaystyle A={\tfrac {3}{2}}{\sqrt {3}}\ z^{2}}$

Dit betreft een zeshoek die op zijn platte kant staat.

• Het isoperimetrisch quotiënt van een regelmatige zeshoek is 0,907.
• Het schläfli-symbool is {6}.

Het vasteland van Frankrijk wordt wel voorgesteld als een regelmatige zeshoek: La France hexagone.^[2] Daarmee is l'Hexagone een cultureel symbool en een bijnaam van het land geworden. Er zat in alle medailles die tijdens de Olympische Zomerspelen van 2024 in Parijs werden uitgereikt een zeshoekig stuk metaal uit de Eiffeltoren verwerkt.^[3]

• 
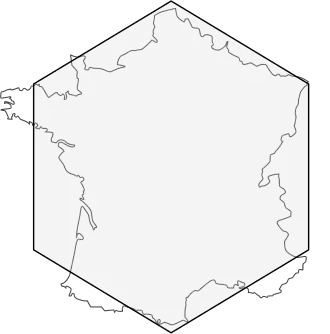  Kaart en zeshoek
• 
  Herdenkingsmunt bij het 30-jarig bestaan van de Vijfde Franse Republiek
• 
  Embleem van de Parti Social Français

Zie de categorie Regular hexagons van Wikimedia Commons voor mediabestanden over dit onderwerp.