Osculatiecirkel

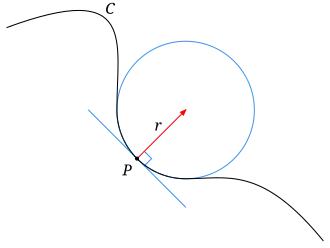
Een osculatiecirkel, krommingscirkel of osculerende cirkel is de cirkel die in een gegeven punt ${\displaystyle P}$ van een kromme die kromme het best benadert, beter dan elke andere cirkel. Men kan de osculatiecirkel beschouwen als de cirkel bepaald door ${\displaystyle P}$ en twee punten op de kromme die infinitesimaal dicht naast ${\displaystyle P}$ liggen. Het middelpunt van de osculatiecirkel noemt men het krommingsmiddelpunt en de straal van de cirkel de kromtestraal. De kromtestraal en de kromming van een kromme door een punt ${\displaystyle P}$ zijn omgekeerd evenredig aan elkaar.

Voor een vloeiende kromme moet de osculatiecirkel in een punt ${\displaystyle P}$ aan de volgende voorwaarden voldoen:

1. ${\displaystyle P}$ is een gemeenschappelijk punt van de kromme en de cirkel
2. in ${\displaystyle P}$ hebben kromme en cirkel dezelfde eerste afgeleide, dezelfde raaklijn,
3. in ${\displaystyle P}$ hebben kromme en cirkel dezelfde tweede afgeleide, zij hebben daar dezelfde kromming.

De wiskundige formulering hiervan resulteert in een stelsel van drie vergelijkingen met drie onbekenden. De drie onbekenden zijn de straal en de twee coördinaten van het middelpunt van de cirkel. ${\displaystyle P}$ en de osculerende cirkel hebben in dit geval een contact van de orde twee.

Het middelpunt van de osculatiecirkel aan een kromme in het punt ${\displaystyle P}$ ligt steeds op de normaalvector van de kromme vanuit ${\displaystyle P}$. De meetkundige plaats van de middelpunten van de osculatiecirkels van alle punten van een kromme is de evolute van de kromme. Dit is tevens de omhullende van de normaallijnen op de kromme.

Deze stelling, genoemd naar Peter Tait en Adolf Kneser die ze onafhankelijk van elkaar ontdekten op het einde van de negentiende en het begin van de twintigste eeuw, stelt dat:

van een kromme met monotoon positieve kromming zijn de osculatiecirkels paarsgewijs disjunct en in elkaar genesteld.

Dit is bijvoorbeeld het geval voor een logaritmische spiraal.^[1]

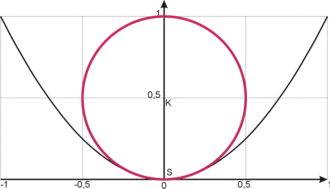
Wanneer de osculatiecirkel met de kromme in punt ${\displaystyle P}$ een contact van derde orde of hoger heeft, zegt men dat het een hyper-osculatiecirkel is. Dit is bijvoorbeeld het geval als de kromme een lokaal minimum of maximum heeft, zoals bij een parabool. Dergelijke punten noemt men een knoop van de kromme. Een knoop op een kromme komt overeen met een singulier punt op de evolute van de kromme.

De stelling van Tait-Kneser geldt alleen voor krommen zonder knopen. Dat zijn noodzakelijkerwijs open krommen, gesloten krommen hebben altijd knopen. Syamadas Mukhopadhyaya heeft in 1909 bewezen dat een vlakke ellips, dit is een vloeiende gesloten strikt convexe kromme, minstens vier knopen heeft.