Muizenprobleem

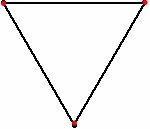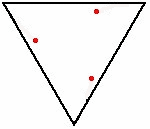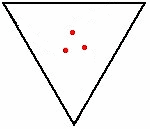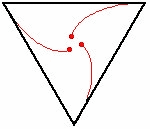
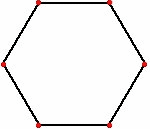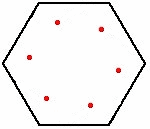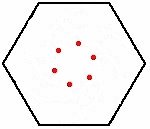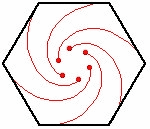
Het muizenprobleem is een wiskundig probleem waarin bijvoorbeeld drie of meer muizen op de hoekpunten van een regelmatige veelhoek staan. Elke muis achtervolgt zijn naaste buur. Alle muizen starten tegelijk en lopen even snel. De vraag is waar en wanneer de muizen op hetzelfde punt bij elkaar komen, welke afstand ze dan hebben afgelegd en welke baan?

Het probleem werd in 1877 met drie honden die op de hoekpunten van een gelijkzijdige driehoek beginnen door Édouard Lucas geformuleerd.^[1] Henri Brocard bewees in 1880^[2] dat de banen die ze volgen logaritmische spiralen zijn, die samenkomen in het middelpunt van de driehoek.

Dit kan worden geïllustreerd voor het geval van vier muizen die elkaar op een vierkant achtervolgen:

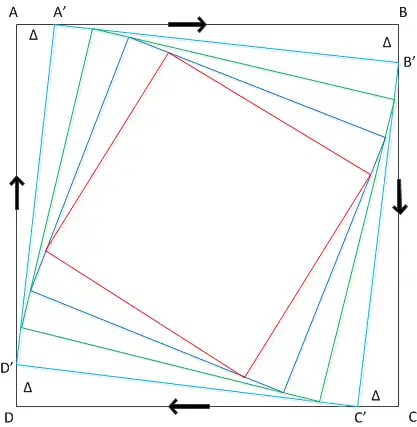
${\displaystyle A}$ achtervolgt ${\displaystyle B}$, ${\displaystyle B}$ achtervolgt ${\displaystyle C}$, ${\displaystyle C}$ achtervolgt ${\displaystyle D}$ en ${\displaystyle D}$ achtervolgt ${\displaystyle A}$. Bij aanvang volgt iedere muis de zijde van het vierkant. Na verloop van een korte tijd ${\displaystyle \Delta }$ bevinden ze zich in posities ${\displaystyle A',B',C'}$ en ${\displaystyle D'}$, de hoekpunten van een nieuw vierkant, en moeten ze hun richting aanpassen. Dit herhaalt zich steeds in realiteit continu, zodat zij op een gegeven moment in het midden van het vierkant bij elkaar komen.

In het algemeen geldt voor ${\displaystyle n}$ muizen in een regelmatige veelhoek met ${\displaystyle n}$ zijden, waarvan de lengte van een zijde gelijk is aan 1, en waarin de muizen bewegen met een snelheid gelijk aan 1, dat de afstand tussen twee naburige muizen met snelheid ${\displaystyle 1-\cos(2\pi /n)}$ vermindert, zodat ze samenkomen na een verlopen tijd van ${\displaystyle 1-\cos(2\pi /n)}$, wat tegelijk de afstand is die ze hebben afgelegd.

Het probleem won aan populariteit toen het in 1950 in het boek Mathematical Snapshots verscheen van Hugo Steinhaus, oorspronkelijk in het Pools in 1937. Diverse varianten zijn bestudeerd, zoals wat als de muizen op de hoekpunten van een niet-regelmatige veelhoek vertrekken, wat als de muizen een verschillende snelheid hebben en wat als ze niet hun naaste buur achtervolgen maar een andere?

Klamkin en Newman hebben in 1971 bewezen dat drie even snelle muizen vanuit de hoekpunten van een willekeurige driehoek elkaar altijd op hetzelfde moment treffen, zolang de drie hoekpunten niet op een lijn liggen.^[3] Behroozi en Gagnon toonden aan dat dit ook voor vier muizen geldt wanneer die van de hoekpunten vertrekken van een convexe vierhoek.^[4]