Menglineair ingeschreven cirkel
Een menglineair ingeschreven cirkel is een cirkel die raakt aan twee zijden van een driehoek ABC en aan de binnenkant de omgeschreven cirkel van ABC.
Bewijs van bestaan
Bewijs 1 (inversie):
Zij gegeven een driehoek ABC en zij Γ de A-aangeschreven cirkel. We inverteren rond A met straal waar b en c respectievelijk de lengte van AC en AB zijn. Vervolgens spiegelen we alles over de bissectrice van hoek BAC. We noteren P' als het punt corresponderend met P na de transformaties. In deze transformatie wordt B naar C gestuurd, C naar B, lijn BC naar de omgeschreven cirkel van ABC en worden lijnen AB en AC omgewisseld. We zien dat Γ' na de transformaties nog steeds aan AB en AC raakt en nu ook aan de omcirkel van ABC raakt, want Γ raakte aan BC. Omdat Γ AB en AC buiten de omgeschreven cirkel van ABC raken, raakt Γ' AB' en AC' juist binnen omgeschreven cirkel AB'C' (dit is dezelfde cirkel als de omcirkel van ABC!). We hebben nu bewezen dat Γ' raakt aan AB' (oftewel AC), aan AC' (oftewel AB) en aan omcirkel AB'C" (oftewel omcirkel ABC). DIt is precies de menglineaire ingeschreven cirkel!
Bewijs 2:
We bekijken weer een driehoek ABC. In dit geval verschuiven we de ingeschreven cirkel, ω, naar de A-aangeschreven cirkel, Ω. We zien dat de ingeschreven cirkel geen snijpunten heeft met de omcirkel van ABC. We zien ook dat Ω twee snijpunten heeft met de omgeschreven cirkel van ABC. Daarnaast zien we dat ω en Ω beide aan AB en AC raken, dus als we de ene cirkel naar de andere verscuhiven, we altijd aan AB en AC blijven raken!
Als we ω naar Ω verschuiven, dan zien we dat de verschuivende cirkel aan het begin nog geen snijpunten heeft met de omcirkel van ABC, maar aan het einde twee snijpunten heeft! Ergens hiertussen zal dus een cirkel zijn die maar 1 snijpunt heeft met ABC omdat het een continue verschuiving is. Deze cirkel is precies de A-menglineair ingeschreven cirkel, omdat hij raakt aan AB, AC en omcirkel ABC!
Constructie
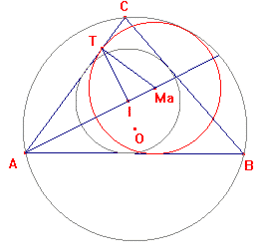
De menglineair ingeschreven cirkel in hoek A, dus rakend aan AB en AC kan als volgt worden geconstrueerd:
- I is het middelpunt van de ingeschreven cirkel van ABC en
- AI is de bissectrice van hoek A.
- T is het punt waar een lijn vanuit I loodrecht op AI de zijde AC snijdt.
- Ma is weer het snijpunt van een loodlijn uit T op bissectrice AI.
- De cirkel met middelpunt Ma door T is de gevraagde cirkel.
De straal ρA van de menglineair ingeschreven cirkel in hoek A is ρA = , met r de straal van de ingeschreven cirkel.
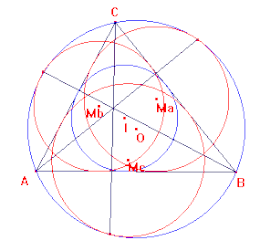
Eigenschappen
De lijnen, die een hoekpunt verbinden met het raakpunt van de corresponderende menglineaire ingeschreven cirkel en omgeschreven cirkel, snijden elkaar in één punt. Het gezamenlijke snijpunt is het driehoekscentrum met kimberlingnummer X(55), het uitwendig gelijkvormigheidscentrum van de ingeschreven cirkel en de omgeschreven cirkel.
Deze drie lijnen snijden elkaar nog steeds in één punt, wanneer in de hele berekening in plaats van de omgeschreven cirkel van ABC een andere, willekeurige cirkel wordt genomen.