Meander (wiskunde)

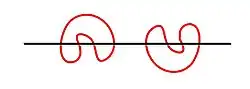
In de wiskunde wordt met meander een configuratie aangeduid van twee krommen in het vlak, die niet zichzelf snijden maar elkaar wel een aantal maal snijden. Wanneer de twee krommen open zijn en homeomorf met een lijn, spreekt men van een open meander. Wanneer een van de twee krommen gesloten is en de andere open, spreekt men van een gesloten meander. De krommen zijn jordan-krommen en voor de eenvoud wordt een ervan steeds als een lijn voorgesteld. Een stelsel van meanders bestaat uit een lijn en een aantal jordan-krommen die elkaar niet snijden.

Een gesloten meander wordt dus gevormd door een gesloten kromme die zichzelf niet snijdt en een lijn. De kromme heeft met de lijn ofwel geen, ofwel een even aantal ${\displaystyle 2n}$ snijpunten. ${\displaystyle n}$ is de orde van de meander.

Het aantal verschillende gesloten meanders met ${\displaystyle 2n}$ snijpunten noemt men het meandrische getal of gesloten-meandrische getal ${\displaystyle M_{n}}$. Hierbij zijn twee meanders verschillend indien men niet door continue vervorming van de kromme van de ene meander naar de andere kan overgaan zonder het aantal of de volgorde van de snijpunten te veranderen.

• ${\displaystyle n=0:M_{0}=1}$, lijn en een cirkel die elkaar niet snijden
• ${\displaystyle n=1:M_{1}=1}$, cirkel die een lijn tweemaal snijdt
• ${\displaystyle n=2:M_{2}=2}$, namelijk:

• ${\displaystyle n=3:M_{3}=8}$:

en hun spiegelingen ten opzichte van de lijn.

Met uitzondering van de gevallen ${\displaystyle n=0}$ en ${\displaystyle n=1}$ zijn de gesloten-meandrische getallen even getallen: de ene helft van de mogelijke configuraties is het spiegelbeeld om de lijn van de andere helft heen.

De eerste meandrische getallen vanaf ${\displaystyle n=0}$ zijn:

1, 1, 2, 8, 42, 262, 1828, 13820, 110954, 933458, 8152860, ...^[1]

Het opsommen van alle mogelijke meanders is een probleem uit de combinatoriek, waarbij het aantal mogelijke configuraties exponentieel stijgt met toenemende voor ${\displaystyle n}$. Alleen de meandrische getallen tot en met ${\displaystyle n=24}$ zijn tot nog toe bekend.^[2]

Voor een stelsel met ${\displaystyle k}$ gesloten krommen wordt het meandrisch getal voorgesteld als ${\displaystyle M_{n}^{(k)}.}$ Voorbeelden:

• voor ${\displaystyle k=2,\ n=2,3,4,5,\ldots }$ is dit de reeks: 2, 12, 84, 640, 5236, 45164...^[3]
• voor ${\displaystyle k=3,\ n=3,4,5,6,\ldots }$ is dit de reeks: 5, 56, 580, 5894, 60312, 624240...

Er geldt:^[3]

${\displaystyle M_{n}^{(n)}={\frac {1}{2n+1}}{\binom {2n+1}{n}}={\frac {(2n)!}{n!(n+1)!}}}$

dit is het ${\displaystyle n}$-de Catalan-getal.

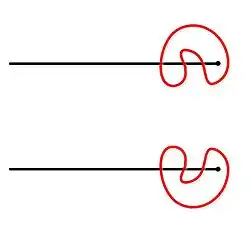
Een open meander van orde voor ${\displaystyle n}$ bestaat uit een open kromme die zichzelf niet snijdt en een lijn, waarbij de kromme de lijn ${\displaystyle n}$ maal snijdt. Twee open meanders worden als gelijkwaardig beschouwd als ze homeomorf zijn in het vlak.

• De enige mogelijke open meander van orde nul bestaat uit twee evenwijdige lijnen.
• De enige mogelijke open meander van orde 1 snijdt de lijn eenmaal:

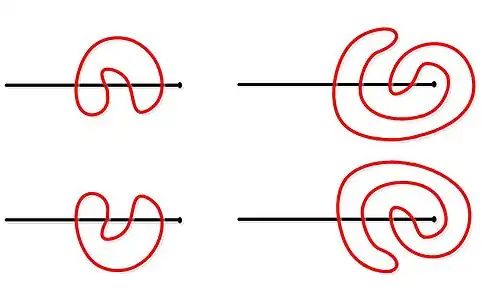
• De open meander van orde 2 snijdt de lijn tweemaal:

Bruce Bobier en Joe Sawada hebben een algoritme ontwikkeld dat snel alle open meanders of meandrische stelsels van orde ${\displaystyle n}$ kan genereren.^[4]

Het aantal verschillende open meanders van orde ${\displaystyle n}$ is het open-meandrisch getal ${\displaystyle m_{n}}$. Dit is het aantal manieren waarop een rivier een weg ${\displaystyle n}$ maal kan kruisen. Hierbij wordt over het algemeen verondersteld dat de kromme vanuit het zuidwesten komt en van west naar oost loopt, met andere woorden minstens een uiteinde heeft dat onder de lijn ligt.

De eerste open-meandrische getallen ${\displaystyle m_{n}}$ vanaf ${\displaystyle n=0}$ zijn:

1, 1, 1, 2, 3, 8, 14, 42, 81, 262, 538, 1828, 3926, 13820, 30694, 110954, ...^[5]

Iwan Jensen^[6] heeft de open-meandrische getallen tot orde ${\displaystyle n=43}$ berekend.

Er is een bijectie tussen een lus, een gesloten kromme, die een lijn in ${\displaystyle 2n}$ punten snijdt en een lijn, een open kromme, die een lijn in ${\displaystyle 2n-1}$ punten snijdt. Er geldt:

${\displaystyle M_{n}=m_{2n}-1}$

Dus de oneven open-meandrische getallen zijn gelijk aan de gesloten-meandrische getallen.

Bij een meander wordt verondersteld dat de lijn aan beide zijden oneindig lang doorloopt. Wanneer de lijn een halve lijn is met een eindpunt en maar aan één zijde oneindig doorloopt, spreekt men van een semi-meander. Hier geldt ook dat twee semi-meanders verschillend zijn als ze niet homeomorf zijn.

Een gesloten semi-meander van orde ${\displaystyle n}$ bestaat uit een gesloten zichzelf niet snijdende kromme die de halve lijn in ${\displaystyle n}$ punten snijdt. ${\displaystyle n}$ kan nu wel oneven zijn bij een gesloten kromme.

Dit zijn de semi-meanders van orde 3:

Dit zijn de semi-meanders van orde 4:

Het aantal verschillende semi-meanders van orde ${\displaystyle n}$ wordt aangeduid door het semi-meandrische getal ${\displaystyle {\overline {M_{n}}}}$.

Wiskundige meanders duiken in diverse studiegebieden op,^[2] waaronder

• vouwproblemen: bijvoorbeeld
  • kaartenvouwprobleem: bepaal het aantal manieren een rechthoekige landkaart kan worden opgevouwen
  • postzegelprobleem: bepaal het aantal manieren waarop een strip postzegels kan worden opgevouwen
  • het aantal manieren waarop polymeerketens kunnen worden opgevouwen^[3]
• Meanders staan in de computerwetenschap in verband met het sorteren van jordan-reeksen, die worden bepaald door de opeenvolgende ${\displaystyle x}$-coördinaten van de snijpunten van een jordan-kromme met de x-as.^[7]
• Ze zijn in de theoretische informatica in verband gebracht met de gray-codering van strings in bepaalde formele talen.^[8]
• bij het opsommen van bepaalde vlakke algebraïsche krommen