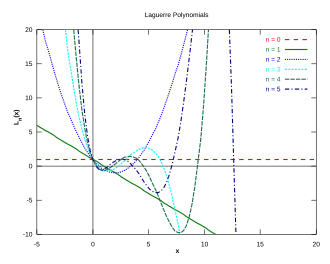
 De eerste 5 laguerre-polynomen.
De eerste 5 laguerre-polynomen.
In de wiskunde zijn de laguerre-polynomen, genoemd naar Edmond Laguerre (1834 - 1886), oplossingen van de  -de differentiaalvergelijking van Laguerre:
-de differentiaalvergelijking van Laguerre:

Laguerre-polynomen vinden toepassing in de kwantummechanica, in het radiële deel van de oplossing van de schrödingervergelijking voor een 1-elektron atoom.
Definitie
De  -de laguerre-polynoom
-de laguerre-polynoom  is een polynoom van de graad
is een polynoom van de graad  die gegeven wordt door de rodriguez-formule:
die gegeven wordt door de rodriguez-formule:

Voor de zo gedefinieerde laguerre-polynomen geldt:

Fysici gebruiken vaak een definitie waarbij  -de laguerre-polynoom een factor
-de laguerre-polynoom een factor  (
( faculteit) groter is.
faculteit) groter is.
De eerste laguerre-polynomen zijn:

|

|
| 0 |

|
| 1 |

|
| 2 |

|
| 3
|

|
| 4
|

|
| 5
|

|
| 6
|

|
Recursie
Tussen de polynomen bestaan de volgende recursieve betrekkingen:

en

Orthogonaliteit
Laguerre-polynomen vormen een orthonormaal stelsel met betrekking tot het inproduct:

Er geldt:

met
 de kronecker delta
de kronecker delta
Contourintegraal
De laguerre-polynomen kunnen in het complexe vlak ook uitgedrukt worden als complexe kringintegraal om de oorsprong, dus als een complexe integraal:

Gegeneraliseerde laguerre-polynomen
De polynoom-oplossingen van de differentiaalvergelijking

worden gegeneraliseerde laguerre-polynomen genoemd.
De formule van Rodriguez voor deze polynomen is

De gewone laguerre-polynomen zijn een speciaal geval:

De eerste gegeneraliseerde laguerre-polynomen zijn:

Externe links
