Indompeling (wiskunde)

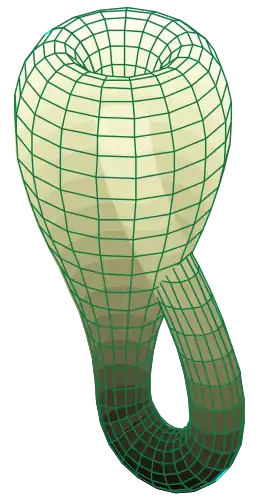
In de wiskunde is een indompeling een differentieerbare afbeelding tussen differentieerbare variëteiten waarvan de afgeleide overal injectief is. Expliciet is f : M → N een indompeling als

${\displaystyle D_{p}f:T_{p}M\to T_{f(p)}N\,}$

een injectieve afbeelding is op elk punt p van M (waar de notatie ${\displaystyle T_{p}X}$ de raakruimte vertegenwoordigt van ${\displaystyle X}$ op het punt ${\displaystyle p}$). Op equivalente wijze is f een indompeling als deze functie een constante rang heeft die gelijk is aan de dimensie van M:

${\displaystyle \operatorname {rang} \,f=\dim M.}$

De afbeelding f zelf hoeft niet injectief te zijn, de afgeleide echter wel.

• Onderdompeling (wiskunde)

• (en) Embeddings and immersions (Inbeddingen en indompelingen), door Masahisa Adachi, in het Engels vertaald door Kiki Hudson
• (en) Smale, S, A classification of immersions of the two-sphere (Een classificatie van indompelingen van de 2-sfeer), Transactions of the American Mathematical Society, 90 1958 281–290.
• (en) Smale, S, The classification of immersions of spheres in Euclidean spaces (De classificatie van indompelingen van sferen in Euclidische ruimten), Ann. of Math. (2) 69 1959 327—344.