Formule van Heron
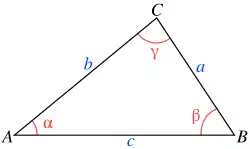
Met de formule van Heron kan de oppervlakte van een driehoek worden berekend, uit de lengtes , en van de zijden van de driehoek:
waarin de semiperimeter de halve omtrek is:
Een andere vorm met ingevuld is:
De formule staat ook bekend als de -formule. De formule van Heron is een speciaal geval van de formule van Brahmagupta. De formule van Brahmagupta geeft de oppervlakte van een koordenvierhoek en een driehoek kan worden gezien als een koordenvierhoek, waarvan twee hoekpunten samenvallen.
Geschiedenis
De formule wordt toegeschreven aan Heron van Alexandrië en een bewijs kan dan ook in zijn boek Metrica uit ongeveer het jaar 60 na Chr. worden gevonden. Er wordt gesuggereerd dat ook Archimedes, die meer dan 200 jaar eerder leefde, de formule al kende.
Een aan de formule van Heron equivalente formule:
werd door de Chinezen onafhankelijk van de Grieken ontdekt. Dit Chinese equivalent werd in 1247 gepubliceerd door de wiskundige Qin Jiushao in zijn Shushu Jiuzhang, 數書九章, Wiskundige verhandeling in negen secties.
- H Hofstede. De formule van Heron.
- D Klingens. De formule van Heron, 21 juli 2010.