Derdemachtswortel

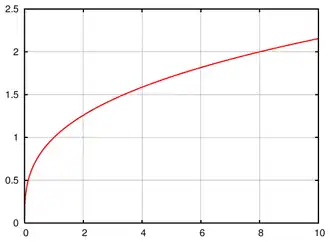
De derdemachtswortel, soms ook kubuswortel, van een reëel getal x, genoteerd als ${\displaystyle {\sqrt[{3}]{x}}}$, is het reële getal ${\displaystyle a}$ dat tot de derde macht verheven gelijk is aan ${\displaystyle x}$. Anders geformuleerd:

${\displaystyle a={\sqrt[{3}]{x}}\Longleftrightarrow a^{3}=x}$

Een andere notatie voor de derdemachtswortel is

${\displaystyle {\sqrt[{3}]{\ x\ }}=x^{\frac {1}{3}}}$

De meeste rekenmachines hebben de mogelijkheid een willekeurige macht van een getal uit te rekenen. Zo is:

${\displaystyle {\sqrt[{3}]{\ 729\ }}=729^{1/3}=9}$

Heron van Alexandrië gaf in zijn boek Metrica in de 1e eeuw al een manier om de derdemachtswortel uit een getal ${\displaystyle x}$ te benaderen, die kan worden geschreven als:

${\displaystyle a+{\frac {bd}{bd+aD}}(b-a)}$,

waarin ${\displaystyle a^{3}<x<b^{3},d=x-a^{3}}$ en ${\displaystyle D=b^{3}-x}$.

Voor derdemachtswortels werden, voordat ze met een rekenmachine konden worden gevonden, speciale tabellen gebruikt om ze mee uit te kunnen rekenen.

		berekening
8	${\displaystyle {\sqrt[{3}]{\ 8\ }}=2}$	${\displaystyle 2^{3}=8}$
125	${\displaystyle {\sqrt[{3}]{\ 125\ }}=5}$	${\displaystyle 5^{3}=125}$
een miljoenste	${\displaystyle {\sqrt[{3}]{\ 0{\ ,\ }000001\ }}=0{\ ,\ }01}$	${\displaystyle 0{\ ,\ }01^{3}=0{\ ,\ }000001}$
27.000	${\displaystyle {\sqrt[{3}]{\ 27.000\ }}=30}$	${\displaystyle 30^{3}=27.000}$
1	${\displaystyle {\sqrt[{3}]{\ 1\ }}=1}$	${\displaystyle 1^{3}=1}$
-64	${\displaystyle {\sqrt[{3}]{\ -64\ }}=-4}$	${\displaystyle (-4)^{3}=-64}$

De derdemachtswortel is ook op te vatten als de oplossing van een derdegraadsvergelijking, ofwel als een nulpunt van een derdegraads polynoom. In het geval van ${\displaystyle {\sqrt[{3}]{\ 125\ }}=5}$ gaat het om de volgende vergelijking:

${\displaystyle x^{3}-125=0}$

Nadat de wortel 5 is gevonden, kunnen we deze vergelijking ontbinden in factoren:

${\displaystyle (x-5)(x^{2}+5x+25)=0}$

Er zijn nog meer wortels, namelijk de oplossingen van de tweede factor, maar die zijn vanwege de negatieve discriminant niet reëel. De twee nulpunten van ${\displaystyle x^{2}+5x+25}$ kunnen als een complex getal worden gedefinieerd.

Het berekenen van een derdemachtswortel is geen basisoperatie zoals optellen of vermenigvuldigen. Een irrationaal getal kan per definitie niet in decimale notatie worden weergegeven, dus is een benadering het best mogelijke. Om met de basisoperaties een benadering van een wortel te vinden wordt daarom een rekenschema een aantal keer herhaald. Dat wordt iteratie genoemd.

Een meetkundig aanschouwelijke aanpak is: de gezochte derdemachtswortel van het getal ${\displaystyle c}$ is de lengte van de zijde van een kubus met inhoud ${\displaystyle c}$. Benader die kubus nu door een rij balken met vierkant grondvlak en vaste inhoud ${\displaystyle c}$. Van elke volgende balk in de rij is de zijde van het grondvlak het gemiddelde van de zijden van zijn voorganger. De hoogte wordt zo gekozen dat de inhoud gelijk blijft.

De gezochte wortel ligt altijd tussen de zijde van het grondvlak en de hoogte van de balk, wat meteen een schatting voor de fout oplevert. Het verschil tussen deze lengtes neemt steeds met meer dan de helft af, de methode convergeert dus snel. Herhaal dit tot de fout voldoende klein is.

Deze rekenmethode is equivalent met de methode van Newton-Raphson, toegepast op de functie ${\displaystyle f(x)=x^{3}-c}$. Het te benaderen nulpunt van deze functie is de derdemachtswortel uit ${\displaystyle c}$.

Een mogelijkheid is ook derdemachtswortels uit te rekenen met een iteratieve methode waarbij alleen de basisoperaties en de vierkantswortel worden gebruikt. ${\displaystyle x^{3}=c}$ kan anders worden geschreven als ${\displaystyle x={\sqrt {\sqrt {\ cx\ }}}}$. Deze vergelijking kan worden gebruikt door een geschikt getal ${\displaystyle x_{0}}$ als startwaarde te nemen en dan steeds te substitueren, waar de volgende waarde uit kan worden berekend:

${\displaystyle x_{n+1}={\sqrt {\sqrt {\ cx_{n}\ }}}}$

Voorbeeld:

${\displaystyle x^{3}=100}$

Kies:

${\displaystyle x_{0}=5}$

vermenigvuldig met ${\displaystyle c=100}$ en bereken:

${\displaystyle x_{1}={\sqrt {\sqrt {\ 500\ }}}=4{,}728708\ldots }$

Ga verder, door steeds het resultaat te vermenigvuldigen met 100 en weer twee keer de wortel te trekken:

${\displaystyle x_{2}={\sqrt {\sqrt {472{,}8708\ldots }}}=4{,}663216\ldots }$

${\displaystyle x_{3}={\sqrt {\sqrt {466{,}3216\ldots }}}=4{,}646986\ldots }$

${\displaystyle x_{2}={\sqrt {\sqrt {464{,}6986\ldots }}}=4{,}642973\ldots }$

${\displaystyle x_{4}={\sqrt {\sqrt {464{,}2973\ldots }}}=4{,}641926\ldots }$

${\displaystyle x_{5}={\sqrt {\sqrt {464{,}1926\ldots }}}=4{,}641673\ldots }$

${\displaystyle x_{6}={\sqrt {\sqrt {464{,}1673\ldots }}}=4{,}641609\ldots }$

${\displaystyle x_{6}={\sqrt {\sqrt {464{,}1609\ldots }}}=4{,}641594\ldots }$

${\displaystyle x_{7}={\sqrt {\sqrt {464{,}1594\ldots }}}=4{,}641590\ldots }$

${\displaystyle x_{8}={\sqrt {\sqrt {464{,}1590\ldots }}}=4{,}641589\ldots }$

Een kubusgetal is omgekeerd een natuurlijk getal dat de derde macht is van een ander natuurlijk getal.