Convex omhulsel

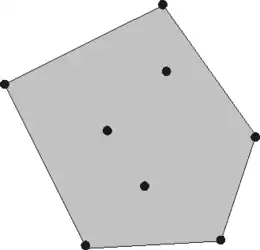
Het convexe omhulsel of de convexe omhulling van een verzameling ${\displaystyle X}$ van punten in de euclidische ruimte, genoteerd als ${\displaystyle \operatorname {conv} X}$, is de kleinste convexe verzameling die ${\displaystyle X}$ omvat. Men kan zich het convexe omhulsel als volgt voorstellen: Als men de punten beschouwt als nagels die in een houten vlak steken, en men een elastiekje rond de nagels spant, dan vormt dat de rand van de convexe omhulling.

Het convexe omhulsel van een verzameling van eindig veel punten is een convexe polytoop: een convexe veelhoek in twee dimensies, een convex veelvlak in drie dimensies. Als alle punten op één lijn liggen is het convexe omhulsel van die punten het lijnstuk tussen de twee punten, die het verst van elkaar liggen.

Het convexe omhulsel van ${\displaystyle X}$ de doorsnede is van alle convexe verzamelingen ${\displaystyle K}$ die ${\displaystyle X}$ omvatten:

${\displaystyle \operatorname {conv} X=\bigcap _{X\subseteq K\subseteq V \atop K\ \mathrm {convex} }K}$

Hierin is ${\displaystyle V}$ de euclidische ruimte.

Het convexe omhulsel is daarmee gelijkwaardig de verzameling van alle convexe combinaties van de punten ${\displaystyle x_{1},\ldots ,x_{n}\in X}$:

${\displaystyle \operatorname {conv} X=\left\{\left.\sum _{i=1}^{n}{\alpha _{i}\cdot x_{i}}\right|x_{i}\in X,n\in \mathbb {N} ,\sum _{i=1}^{n}\alpha _{i}=1,{\alpha _{i}}\geq 0\right\}}$

Er zijn verschillende algoritmes bekend voor het bepalen van de convexe omhulling van een eindige verzameling punten of van andere verzamelingen. Die algoritmes elimineren de punten ${\displaystyle x_{i}}$ uit de gegeven verzameling punten ${\displaystyle x_{1},\dots ,x_{n}}$ die een lineaire combinatie zijn van tenminste twee van de andere punten en dezelfde punten op een na op het convexe omhulsel, die meer dan een keer voorkomen. De complexiteit of rekentijd van deze algoritmes wordt gewoonlijk uitgedrukt in termen van ${\displaystyle n}$, het aantal punten in de verzameling, en ${\displaystyle h,}$ het aantal punten op de convexe omhulling.

Voor punten in twee of drie dimensies zijn algoritmen bekend die de convexe omhulling berekenen met een looptijd in de orde ${\displaystyle O(n\log h)}$. Voor hogere dimensies ${\displaystyle d}$, is de looptijd van de orde ${\displaystyle O(n^{\lfloor d/2\rfloor }).}$

Nog een andere equivalente definitie van convex omhulsel is: de doorsnede van alle halfruimtes die ${\displaystyle X}$ bevatten.

Het bepalen van het convexe omhulsel is een elementair probleem in de computationele geometrie. Het is een voorbereidende stap in veel algoritmes, bijvoorbeeld bij het bepalen van de diameter van een verzameling punten, de grootste afstand tussen twee punten in de verzameling. Die twee punten zullen steeds op het convexe omhulsel van de verzameling liggen. Het volstaat dus om de punten op het convexe omhulsel te bepalen en daarvan de twee punten te zoeken die het verst van elkaar liggen. Voor het bepalen van Voronoi-diagrammen maakt men ook gebruik van convexe omhulsels.